記錄學習內容。看網路上大大們的文章和影片，做些紀錄。
以下內容大多來自網路上大大們的文章。截圖也來自文章和影片。
還不了解，內容可能有錯誤。

[New] Matrix Chain Multiplication using Dynamic Programming Formula
https://www.youtube.com/watch?v=_WncuhSJZyA&list=PLDN4rrl48XKpZkf03iYFl-O29szjTrs_O&index=51&ab_channel=AbdulBari

Matrix Chain Multiplication | DP-8
https://www.geeksforgeeks.org/matrix-chain-multiplication-dp-8/

矩陣A1 = 2row , 3col

矩陣A2 = 3 , 4

矩陣A3 = 4 , 2

A1 * A2 的運算次數 : 2 * 3 * 4 = 24 ，矩陣變成 2 , 4

A2 * A3 的運算次數 : 3 * 4 * 2 = 24 , 矩陣變成 3 ,2

雖然A1 * (A2 * A3) ，( A1 * A2) * A3 ，最後結果一樣 ，但是運算次數是不同的 :

A1 * (A2 * A3) = (2,3) * (3 ,2) -- > 2 * 3 * 2 = 12
12 在加 24 = 36

( A1 * A2) * A3 = (2,4) * (4 ,2) -- > 2 * 4 * 2 = 16
16 在加 24 = 40

Matrix Chain Multiplication using Dynamic Programming :
是用動態規劃的方式。一堆矩陣相乘，比較所有相乘順序，選 運算次數最小的那個數字。

矩陣鏈乘積
https://zh.wikipedia.org/wiki/%E7%9F%A9%E9%99%A3%E9%8F%88%E4%B9%98%E7%A9%8D

Matrix Chain Multiplication | DP-8
https://www.geeksforgeeks.org/matrix-chain-multiplication-dp-8/

輸入是 :

  Input: p[] = {10, 20, 30, 40, 30}

代表這4個矩陣: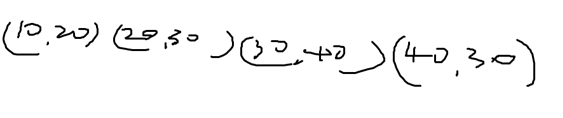

相乘順序的方法(第一項才開始算矩陣):

I =1 ，代表第1個矩陣
k =1 ，代表第1個矩陣 到 第k個矩陣相乘 。

j=4 ，代表第4個矩陣
k=1 ，代表第k+1個矩陣 到 第j個矩陣相乘

像是
10( 20 ) (30 40 30) 代表 第1個矩陣相乘 和 第2到第4矩陣相乘 。
最後 在 這兩個答案 ，做矩陣相乘。

矩陣相乘的方法:

p[i-1] * p[k] * p[j]。
像是 i 2 j 3 k 2
代表 第2個矩陣  和 第3個矩陣相乘 。
會先分為 第2個矩陣 自己相乘 ，第3個矩陣自己相乘 ，都是0 之後
執行p[i-1] * p[k] * p[j]
p[1] * p[2] * p[3] 。 就會是答案。
 
這樣就是結果了 ， 然後每個答案都去更新最小值 。

這種算法，時間複雜度 應該是 O(2的n次方) (不確定)

來看一下列出所有組合 。 
現在有3個矩陣:
A(BC)   (AB)C  

現在有4個矩陣:
A(B(CD))   A((BC)D)   (AB)(CD)   (A(BC))D   ((AB)C)D

現在有5個矩陣，是幾個???:

跟這個有關:
卡塔蘭數
https://zh.wikipedia.org/wiki/%E5%8D%A1%E5%A1%94%E5%85%B0%E6%95%B0

卡塔蘭數為：1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796...

Counting Lesson 6: Catalan Numbers
https://www.youtube.com/watch?v=i5V21WCHTVo&ab_channel=djdmath

(0,0) 到 (5,5) 的通常想法會是 10!/ 5!(5個N不用排列) 5! (5個E不用排列)
也就是 C 10 取 5 ?

但是現在不能 超過 y=x ， 所以 要扣掉一些狀況 。

超過的狀況如教學的圖:
就是說 超過的部分 ，顛倒後 都會變成 x有4個 ，y有6個。就是扣掉 C 10 取4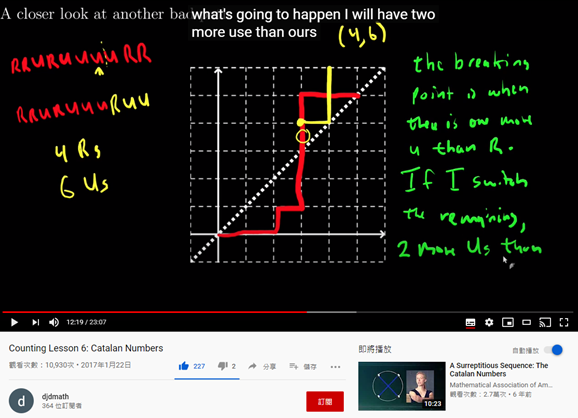

比較好記的方法就是 扣掉 C 10 取4 ，因為 y(6) > x(4)

(3,3)的答案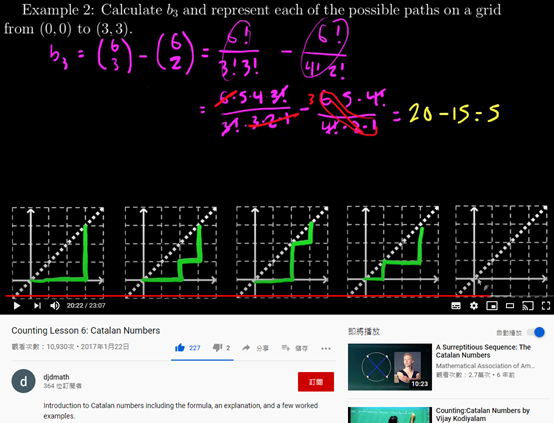

在回到

現在有4個矩陣:
A(B(CD))   A((BC)D)   (AB)(CD)   (A(BC))D   ((AB)C)D

現在有5個矩陣，有幾種算法???:

想成這樣:
(A(B(CD)))   (A((BC)D))   ((AB)(CD))   ((A(BC))D)   (((AB)C)D)

數字不用理 ，因為數字站著不動 。
只要看括號 ，每一步 左括號 都 >= 右括號
所以跟上面 (3,3)的答案 一樣

現在有5個矩陣:
((A(B(CD)))E)

就會是(4,4)的答案

重複算的部分，文章中的圖(綠色的部分就是重複算的地方) :

來看程式
看不懂這個:

m = [[0 for x in range(n)] for x in range(n)]

意思應該是:
例如2維陣列 [2][4]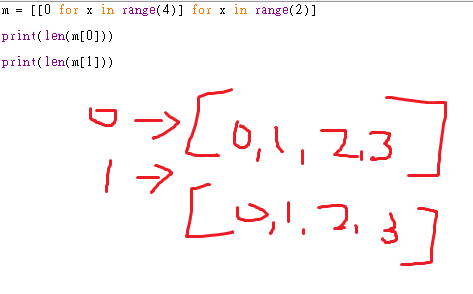

接著看:

第一個迴圈 代表 有幾個矩陣相乘 。
像是 A　*　B　* Ｃ
會先取 兩個矩陣 開始算 ，這樣到 三個矩陣相乘的時候，就可以 用兩個矩陣的結果 拿來算。

第二個迴圈 是 開頭的矩陣 。

第三個迴圈是 開頭 和 結尾的矩陣，之間有幾項。

像是 第1 和第4個矩陣 ， 可以有11 14 、12 24 、13 34 算法

最後的結果 會是 第一個矩陣 * 最後一個矩陣 。
所以取 第1個陣列 的最後一個值

時間複雜度: O(n^3)
空間複雜度: O(n^2)

簡單記: O(n^3) --- >三個迴圈
O(n^2) --- >二維陣列